Trong chương trình toán học phổ thông, đặc biệt là hình học không gian lớp 12, khái niệm đối xứng đóng vai trò nền tảng. Việc nắm vững khái niệm mặt phẳng đối xứng là gì này không chỉ giúp bạn giải nhanh các bài toán trắc nghiệm mà còn rèn luyện tư duy logic, khả năng quan sát thực tế hiệu quả qua bài viết tại hanoi1000.vn.
Khái niệm mặt phẳng đối xứng là gì?
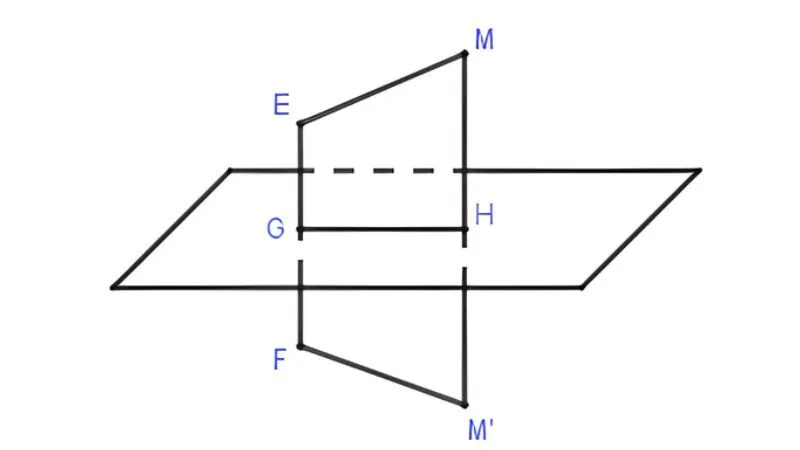
Mặt phẳng đối xứng là mặt phẳng chia một hình hoặc một khối thành hai phần sao cho mỗi điểm ở phần này có một điểm tương ứng ở phần kia, và hai điểm đó đối xứng nhau qua mặt phẳng. Khoảng cách từ hai điểm đối xứng đến mặt phẳng là bằng nhau và đoạn thẳng nối hai điểm vuông góc với mặt phẳng.
Có thể hiểu một cách trực quan rằng, nếu coi mặt phẳng đối xứng như một tấm gương thì hai nửa của hình là hình ảnh phản chiếu hoàn toàn của nhau. Nếu gấp hình theo mặt phẳng đó, hai phần sẽ trùng khít. Một hình có thể có một mặt phẳng đối xứng, nhiều mặt phẳng đối xứng hoặc không có mặt phẳng đối xứng nào, tùy vào cấu tạo và mức độ đều của hình.
Mặt phẳng đối xứng của các khối hình thường gặp
Sau khi đã hiểu rõ mặt phẳng đối xứng là gì, việc quan trọng tiếp theo là nhận diện mặt phẳng đối xứng trong các khối hình quen thuộc. Đây là phần kiến thức xuất hiện rất nhiều trong bài tập và đề thi. Nếu nắm chắc đặc điểm đối xứng của từng khối, người học sẽ làm bài nhanh hơn và tránh được những sai sót không đáng có.
>>> Điều Cần Biết: 114 Là Số Điên Thoại Gì? Các Số Điện Thoại Khẩn Cấp Tại Việt Nam
Mặt phẳng đối xứng của hình lập phương
Hình lập phương là khối hình tiêu biểu cho tính đối xứng trong không gian và thường được dùng làm ví dụ đầu tiên khi học về mặt phẳng đối xứng. Nhờ các cạnh bằng nhau và các mặt hoàn toàn giống nhau, hình lập phương có cấu trúc rất cân đối. Chính vì vậy, số lượng mặt phẳng đối xứng của khối hình này là khá lớn.
- Hình lập phương có 9 mặt phẳng đối xứng
- Có 3 mặt phẳng song song với các cặp mặt đối diện
- Có 6 mặt phẳng đi qua các đường chéo của các mặt
- Tất cả các mặt phẳng đối xứng đều đi qua tâm của hình lập phương
Mặt phẳng đối xứng của hình hộp chữ nhật
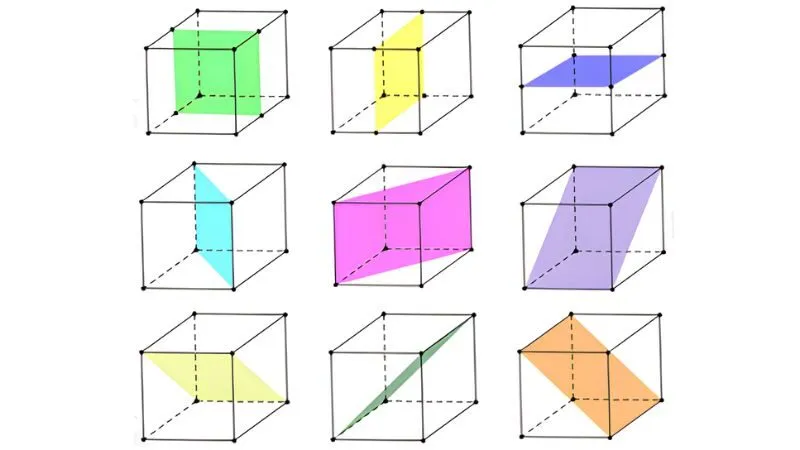
Hình hộp chữ nhật là khối hình quen thuộc, xuất hiện nhiều trong các bài toán thực tế. So với hình lập phương, các cạnh của hình hộp chữ nhật có thể khác nhau về độ dài, khiến tính đối xứng giảm đi. Tuy vậy, khối hình này vẫn có những mặt phẳng đối xứng cơ bản và dễ nhận biết.
- Hình hộp chữ nhật có 3 mặt phẳng đối xứng
- Mỗi mặt phẳng đều đi qua tâm của khối hình
- Các mặt phẳng đối xứng song song với các cặp mặt đối diện
- Sự khác nhau về độ dài các cạnh không làm thay đổi số mặt phẳng đối xứng
Mặt phẳng đối xứng của hình cầu
Hình cầu là khối hình có mức độ đối xứng cao nhất trong hình học không gian. Khi quan sát hình cầu từ bất kỳ hướng nào, ta đều thấy hình dạng giống nhau. Điều này xuất phát từ việc mọi điểm trên bề mặt hình cầu đều có vị trí cân bằng quanh tâm.
- Hình cầu có vô số mặt phẳng đối xứng
- Mọi mặt phẳng đi qua tâm hình cầu đều là mặt phẳng đối xứng
- Không tồn tại mặt phẳng đối xứng nào không đi qua tâm của hình cầu
Mặt phẳng đối xứng của hình trụ
Hình trụ là khối hình thường gặp trong đời sống, từ các vật dụng đơn giản cho đến các chi tiết máy phức tạp. Khi quan sát hình trụ, ta dễ dàng nhận thấy khối hình này đối xứng theo nhiều hướng khác nhau. Tính đối xứng của hình trụ thể hiện rõ cả theo chiều dài trục và theo mặt cắt ngang.
- Hình trụ có vô số mặt phẳng đối xứng
- Các mặt phẳng đi qua trục của hình trụ đều là mặt phẳng đối xứng
- Có một mặt phẳng đối xứng vuông góc với trục và đi qua trung điểm chiều cao
Mặt phẳng đối xứng của hình nón
Hình nón tròn xoay là khối hình quen thuộc trong hình học và cũng xuất hiện nhiều trong thực tế. Khi quan sát hình nón theo trục, ta có thể nhận ra rằng hình được chia thành hai phần hoàn toàn giống nhau. Đây chính là biểu hiện rõ ràng của mặt phẳng đối xứng.
- Hình nón tròn xoay có vô số mặt phẳng đối xứng
- Các mặt phẳng đối xứng đều đi qua trục của hình nón
- Mỗi mặt phẳng chia hình nón thành hai phần trùng khít
Mặt phẳng đối xứng của hình chóp đều
Khác với các khối tròn xoay, tính đối xứng của hình chóp đều phụ thuộc trực tiếp vào hình dạng của đáy. Nếu đáy là đa giác đều, khối hình sẽ có những mặt phẳng đối xứng tương ứng. Vì vậy, khi xét mặt phẳng đối xứng của hình chóp đều, cần chú ý đến số cạnh của đáy.
- Số mặt phẳng đối xứng bằng số cạnh của đa giác đáy
- Mỗi mặt phẳng đối xứng đều đi qua đỉnh chóp
- Mặt phẳng đối xứng đi qua trung điểm của một cạnh đáy
Mẹo ghi nhớ và phương pháp giải bài tập nhanh
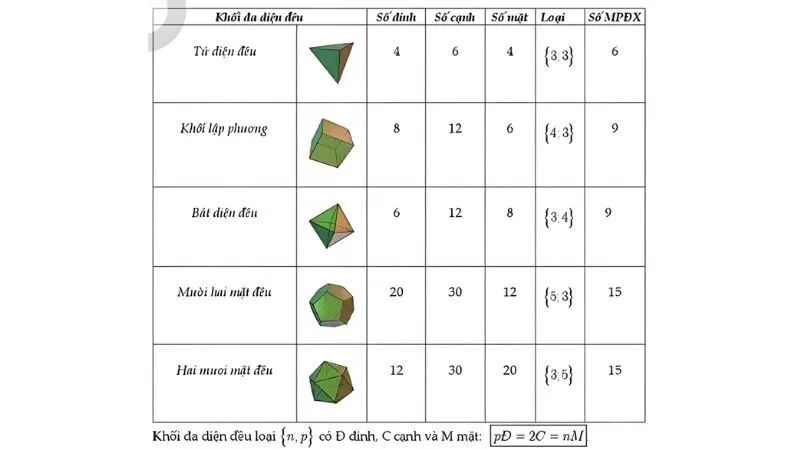
Khi đối mặt với áp lực phòng thi, việc nhầm lẫn giữa số 6, 9 hay 4 là điều rất dễ xảy ra. Để giải quyết vấn đề này, bạn cần xây dựng một hệ thống ghi nhớ dựa trên đặc điểm cấu tạo thay vì học vẹt các con số khô khan. Sau đây là bảng tổng hợp “thần thánh” giúp cho các bạn học sinh dễ ghi nhớ hơn.
| Hình khối | Số mặt phẳng đối xứng |
| Tứ diện đều | 6 |
| Khối lập phương | 9 |
| Bát diện đều | 9 |
| 12 mặt đều / 20 mặt đều | 15 |
| Chóp tứ giác đều | 4 |
| Lăng trụ tam giác đều | 4 |
Những lỗi sai thường gặp khi xác định mặt phẳng đối xứng
Sai lầm lớn nhất của học sinh khi học về mặt phẳng đối xứng là gì chính là việc không phân biệt được “trục đối xứng” và “mặt phẳng đối xứng”. Một hình có thể có trục đối xứng nhưng chưa chắc đã có mặt phẳng đối xứng và ngược lại.
Ví dụ, một hình lăng trụ xiên thường không có mặt phẳng đối xứng nào dù đáy là tam giác đều. Hay nhiều bạn quên mất mặt phẳng “cắt ngang” ở các hình lăng trụ đứng. Để tránh lỗi này, hãy luôn kiểm tra hai hướng: hướng dọc (chứa trục) và hướng ngang (vuông góc với các cạnh bên). Một quy tắc vàng là: Hãy luôn vẽ nháp và thử tưởng tượng việc “gập” hình theo mặt phẳng đó xem các đỉnh có trùng khít lên nhau không.
Kết luận
Hiểu rõ mặt phẳng đối xứng là gì không chỉ giúp bạn hoàn thành tốt các bài tập toán học mà còn mở ra cái nhìn thú vị về sự vận hành của thế giới vật chất xung quanh. Tính đối xứng chính là sự hài hòa, là tiêu chuẩn của cái đẹp trong cả nghệ thuật và khoa học. Hy vọng bài viết này của hanoi1000.vn đã cung cấp cho bạn một cái nhìn toàn diện và sâu sắc nhất về chủ đề này.
